Water Pressure
Definition and how to find it
Water Pressure is the force of the water flowing through the line. In all water lines, this force is essential to ensure the water reaches its destination.
With water dosing, pressure is an essential factor. Some machines won’t work without a certain amount, while others can’t dose if the pressure is too high. Therefore, choosing the right dosing machine for a job means working out your water pressure.
As with the other Golden Numbers, there are a few different ways (depending on your water supply) to find out your water pressure:
- Mains Pressure: If your water will be delivered under mains pressure, this would be around 72 PSI, 4.8 BAR, or 496 kPa. Pressures may differ slightly, but this figure is usually a fairly accurate guide.
- Pump Driven: If your water is delivered from an electric pressure pump, there will usually be a minimum and maximum operating pressure listed somewhere on the pump.
- Gravity Fed: Even if your water comes from a gravity-fed system (like a raised header tank), there is a simple formula for working out your likely water pressure.
Example 1
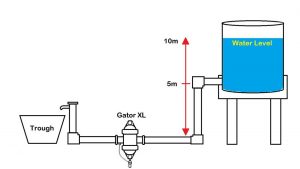
In the diagram above, you will see an basic example of a gravity fed water system. The tank is elevated on a tank stand and the water line runs along the ground. Set up at ground level is a Gator XL water medicator.
So, the total height difference between the water level (when the tank is full) and the injection point is 10 metres. If we divide this height difference by 10, we get an approximate water pressure in BAR.
The pressure (when this tank is full) is 1 bar or 15 PSI.
But as the water level in the tank drops, the water pressure will also drop. When the tank is nearly empty (at a level of 5 metres), the water pressure will be only 0.5 BAR or 7.5 PSI
Example 2
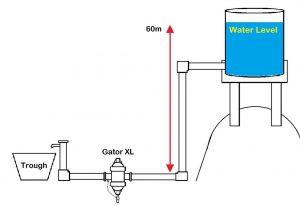
In the diagram above, you will see a similar example, but this time the tank is elevated a further 50m by a hill.
This time, the height difference between the water level in the tank and the injection point is 60 metres. If we divide this height difference by 10, we get an approximate water pressure in BAR.
The pressure in this example is 6 bar or 90 PSI when the tank is full. Once again, this pressure will get lower as the water level drops, but because of the added height of the hill, this will be less significant than in the last example.
See how it works?
Formula

